Optimise cross-products on x86

Let’s dive into the three methods for computing the cross product in 3D using C++.

• Function passing float by reference:

  void crossProduct(float& rx, float& ry, float& rz, float ax, float ay, float az, float bx, float by, float bz) {
      rx = ay * bz - az * by;
      ry = az * bx - ax * bz;
      rz = ax * by - ay * bx;
  }
  

  In this method, we pass the result vector components (rx, ry, rz) by reference and the input vector components (ax, ay, az, bx, by, bz) by value.

• Function passing by value a Vector3D:

  struct Vector3D {
      float x, y, z;
  };
  
  Vector3D crossProduct(Vector3D a, Vector3D b) {
      Vector3D result;
      result.x = a.y * b.z - a.z * b.y;
      result.y = a.z * b.x - a.x * b.z;
      result.z = a.x * b.y - a.y * b.x;
      return result;
  }
  

  In this approach, we define a Vector3D struct to represent a 3D vector. The crossProduct function takes two Vector3D objects by value and returns the resulting Vector3D. The cross product is computed using the standard formula, and the result is stored in a new Vector3D object, which is then returned.

• SIMD with intrinsics for x86 and data passed by value:

  __m128 crossProduct(float ax, float ay, float az, float bx, float by, float bz) {
      __m128 a = _mm_set_ps(0, az, ay, ax);
      __m128 b = _mm_set_ps(0, bz, by, bx);
  
      __m128 a_yzx = _mm_shuffle_ps(a, a, _MM_SHUFFLE(3, 0, 2, 1));
      __m128 b_yzx = _mm_shuffle_ps(b, b, _MM_SHUFFLE(3, 0, 2, 1));
      __m128 c = _mm_sub_ps(_mm_mul_ps(a, b_yzx), _mm_mul_ps(a_yzx, b));
  
      return _mm_shuffle_ps(c, c, _MM_SHUFFLE(3, 0, 2, 1));
  }
  

  This method utilizes SIMD (Single Instruction, Multiple Data) instructions available on x86 architectures. We use the **m128 data type to represent a vector of four single-precision floating-point values. The input vector components are loaded into **m128 variables using _mm_set_ps. Then, we perform a series of shuffles and multiplications to compute the cross product using SIMD instructions. Finally, the result is shuffled to match the desired order and returned as an __m128 value.

Comparison

• The first method, passing floats by reference, is straightforward and easy to understand. It directly computes the cross product using the standard formula and stores the result in the referenced variables. It is readable code since only the edited values are passed by reference.
• The second method, passing by value a Vector3D, provides a more structured approach by encapsulating the vector components into a struct. It allows for better code organization and readability. The performance is similar to the first method.
• The third method, using SIMD instructions, takes advantage of the parallel processing capabilities of x86 architectures. By utilizing SIMD instructions, it can perform multiple floating-point operations simultaneously, potentially leading to faster execution. However, the code is more complex and less readable compared to the other methods.

Performance

In terms of performance, the SIMD method is likely to be the fastest, especially when computing cross products for a large number of vectors. However, the actual performance gains may vary depending on the specific hardware. So, what’s the next step? Before rewriting your whole codebase to support SIMD, you should profile your code.

How about doubles?

SIMD for x86 (using AVX):

__m256d crossProduct(double ax, double ay, double az, double bx, double by, double bz) {
    __m256d a = _mm256_set_pd(0, az, ay, ax);
    __m256d b = _mm256_set_pd(0, bz, by, bx);

    __m256d a_yzx = _mm256_permute4x64_pd(a, _MM_SHUFFLE(3, 0, 2, 1));
    __m256d b_yzx = _mm256_permute4x64_pd(b, _MM_SHUFFLE(3, 0, 2, 1));
    __m256d c = _mm256_sub_pd(_mm256_mul_pd(a, b_yzx), _mm256_mul_pd(a_yzx, b));

    return _mm256_permute4x64_pd(c, _MM_SHUFFLE(3, 0, 2, 1));
}

For double-precision SIMD, we use AVX (Advanced Vector Extensions) instructions, which operate on 256-bit registers. The __m256d data type represents a vector of four double-precision floating-point values. The computation is similar to the single-precision SIMD version, but we use AVX-specific intrinsics like _mm256_set_pd, _mm256_permute4x64_pd, _mm256_mul_pd, and _mm256_sub_pd. Comparison:

• The first and second methods remain straightforward and easy to understand, with the only change being the use of double instead of float. The performance characteristics are similar to their single-precision counterparts.
• The third method, using AVX instructions, takes advantage of the wider 256-bit registers available in modern x86 processors. It allows for parallel processing of four double-precision floating-point values simultaneously. This can lead to improved performance when computing cross products for a large number of vectors.

It’s important to note that the performance gains from using SIMD instructions may vary depending on the specific hardware and the overall structure of your program. In some cases, the compiler may automatically optimize the code to use SIMD instructions when appropriate. When working with double-precision floating-point values, the choice between these methods depends on your specific requirements for precision, performance, and code readability. If precision is crucial and you don’t have strict performance constraints, using double with the first or second method can be a good choice. If performance is a priority and you are targeting x86 architectures with AVX support, the SIMD method can provide a significant speed boost.

What’s next?

If your profiling shows that significant time is spent in simple operations, then you have an easy start learning and implementing SIMD. Take a look at Amdahl’s law to get an estimated of what speed-up you can achieve.

A coursework from Cornell University gives this simple graphs to anticipate what performance boost you can expect from SIMD.

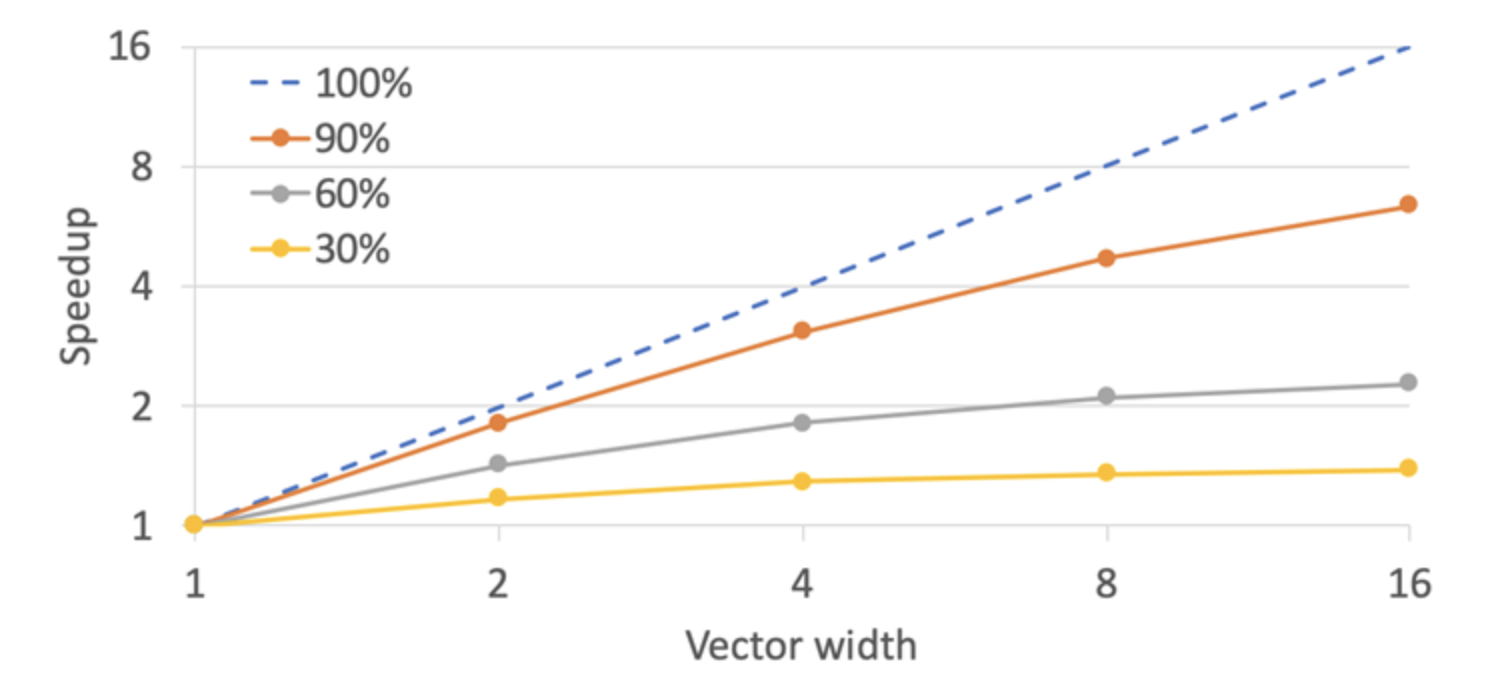
If you vector width accommodates 4 floats and the hot-section of your code is well suited for SIMD parallelization, you can expect up to x3.5 gain.

Writing SIMD code is a hard skill that takes a lot of time to master and it is a low-level optimization extremely close to the hardware. While openmp offers a standard way to implement SIMD, and soon the C++ standard will complement that, the less close you are to a standard, the more performance you can squeeze. Make sure the investment is worth you time before committing to it.